Optimization Method for Weighting Explicit and Latent Concepts in Clinical Decision Support Queries

paper: “Optimization Method for Weighting Explicit and Latent Concepts in Clinical Decision Support Queries” (pdf)

Introduction:

• Information retrieval component that can take a query describing a patient case and find articles in collections of biomedical literature, which are relevant to the given case, is an important part of clinical decision support systems.
• Accurately answering case-based queries requires such as queries in medical domain capturing many explicit and latent aspects of complex information needs underlying such queries.
• Explicit medical concepts are found in the query itself, while latent concepts can be obtained from top-retrieved documents and medical knowledge bases.

Example of CDS Queries:

Query: 26-year-old obese woman with bipolar disorder, on zolpidem and lithium, with recent difficulty sleeping, agitation, suicidal ideation, and irritability

Explicit concepts: “obesity”, “woman”, “biopolar disorder”, “Zolpidem”, and “agitation”.

Latent concepts: “psychotic depression”, “manic disorder”, “dyssomnia”, and “restlessness”.

Example of CDS Queries’ Structure:

Objective:

Develop an intelligent retrieval system that combines query analysis and expansion by jointly determining the importance weights of explicit and latent query concepts depending on their type and source

Challenges:

1. How to identify all effective latent concepts in noisy top retrieved documents and dense knowledge graphs?
2. How to determine the relative importance of unigram, bigram, and multi-term explicit and latent concepts that are extracted from the query itself and top documents retrieved based on a given query as well as the ones that are found in medical knowledge bases?

Concept Sources and their Types:

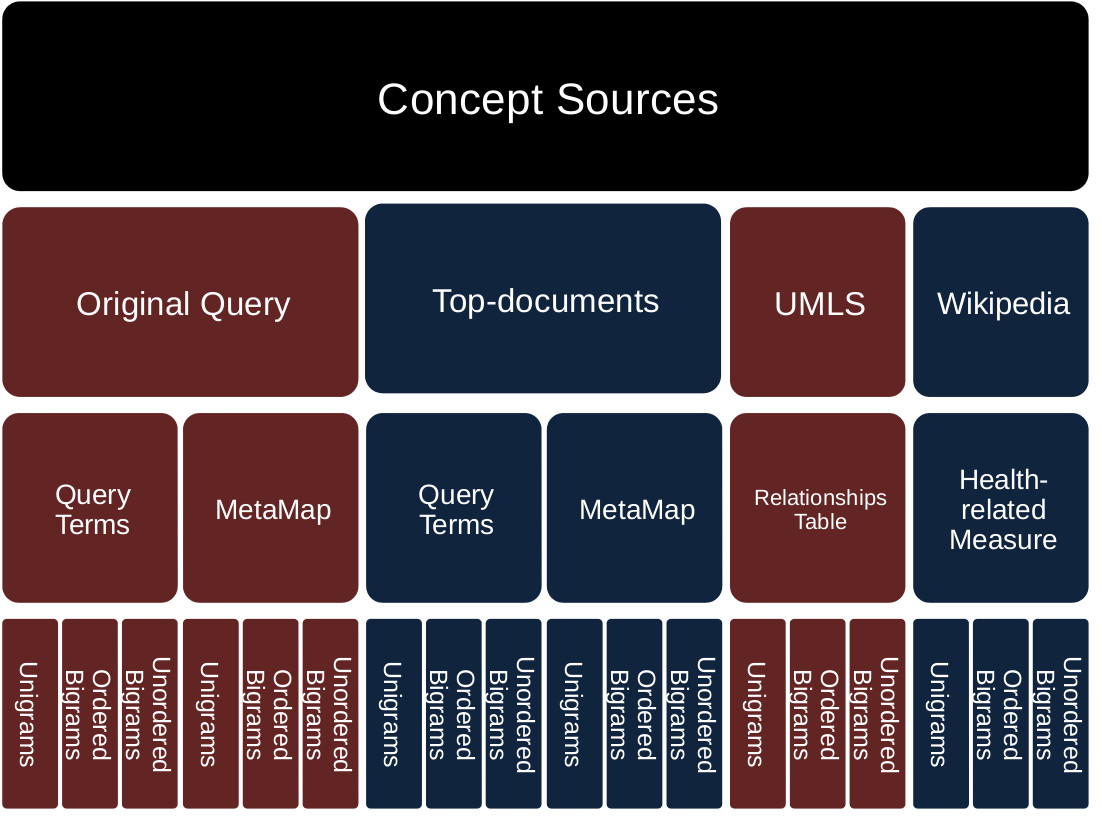
Features that can be used to weigh explicit and implicit a concept c:

1. TF-IDF of concept c in the collection
2. Average collection co-occurrence of concept c with other concepts in the query
3. Maximum collection co-occurrence of concept c with other concepts in the query
4. Number of top retrieved documents containing concept
5. Sum of retrieval scores of top-ranked documents containing concept c
6. Maximum co-occurrence of concept c with other query concepts in top retrieved documents
7. Average co-occurrence of concept c with other query concepts in top retrieved documents
8. Do infoboxes of Wikipedia articles corresponding to concept c contain any health-related keywords?
9. Does any of the terms of concept c exist in the title of any Wikipedia health-related articles?
10. Average distance between concept c in the UMLS concept graph and other query, top document and related UMLS concepts identified for a query
11. Popularity (or node degree) of concept c in the UMLS concept graph
12. Direction of concept c with respect to query concepts in the UMLS semantic network
13. Does concept c have a UMLS semantic type that is effective for medical query expansion?

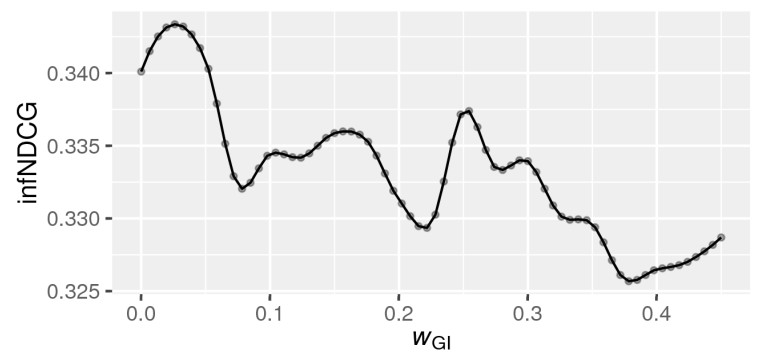
Objective Function:

The Objective Function to find the weights of concepts can be nonconvex:

Graduated Optimization Method:

• Graduated optimization is an iterative optimization method.
• It gradually finds the global optimum of a given objective function by finding the optima for a series of simplified objective functions.
• Each of these simplified objective functions is obtained from the original objective function by applying different degree of smoothing to make the original function more convex.
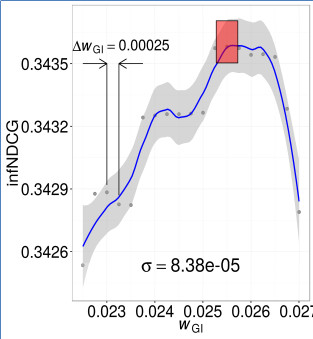
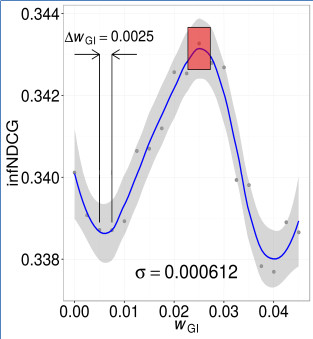
• It starts from the solution to the most simplified optimization problem (i.e., when the maximum degree of smoothing is applied to the original objective function) and considers this solution as the starting point for the second less simplified problem (i.e. less smoothed original objective function).
• This process continues until the global optimum for the original objective function is found. This procedure is based on the assumption that the global optimum of a given objective function at the current iteration is close enough to its global optimum at the next iteration. Therefore, at the next iteration, the region of the parameter space that is far enough from the optimum point at the current iteration is ignored. As a result, a smaller region that is close to the optimum point at the current iteration is searched for the optimal parameter setting at the next iteration.

First Iteration	Second Iteration	Third Iteration